Memahami Algoritma Principal Component Analysis (PCA) dalam Data Science

Pendahuluan

Dalam dunia data science, teknik untuk mengurangi dimensi data menjadi sangat penting, terutama ketika kita menghadapi dataset besar dengan banyak fitur. Salah satu metode yang paling terkenal untuk mencapai ini adalah Principal Component Analysis atau PCA. PCA merupakan teknik yang digunakan untuk mengubah data yang memiliki banyak dimensi menjadi data dengan dimensi lebih rendah namun tetap mempertahankan informasi penting dari data asli. Artikel ini akan membahas konsep dasar PCA, bagaimana cara kerjanya, dan aplikasinya dalam analisis data.

Apa itu Principal Component Analysis (PCA)?

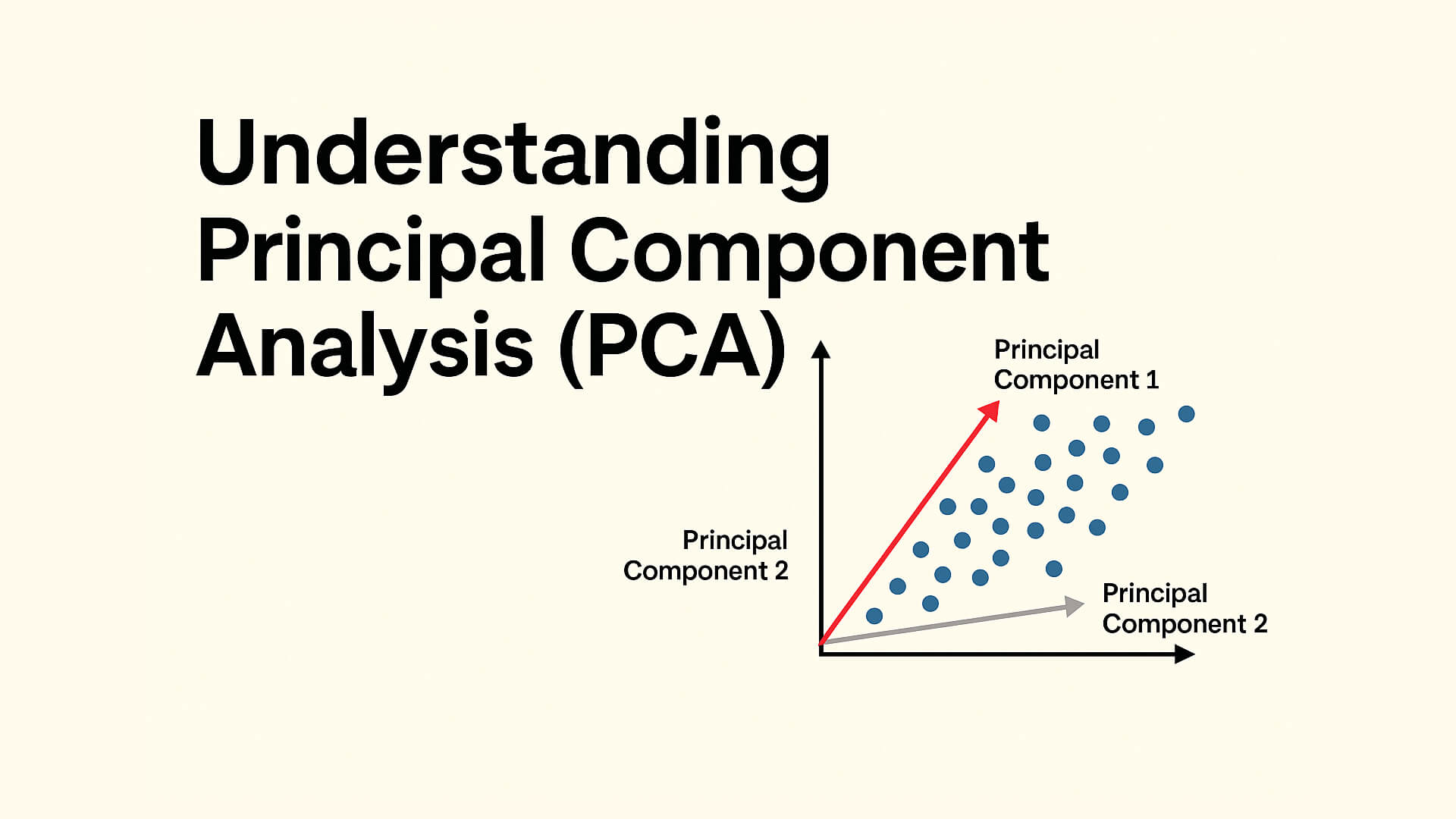
Principal Component Analysis (PCA) adalah teknik statistik yang digunakan untuk mengurangi dimensi data dengan cara mengidentifikasi arah terbesar dari variansi dalam data. Dengan kata lain, PCA mencari kombinasi linier dari variabel asli yang paling banyak menggambarkan data. Setiap kombinasi linier ini disebut sebagai principal component.

Pada umumnya, PCA digunakan ketika kita memiliki data dengan banyak fitur, tetapi tidak semua fitur tersebut diperlukan untuk analisis lebih lanjut. PCA membantu kita untuk menemukan fitur utama yang dapat mewakili data dalam dimensi yang lebih rendah, sehingga lebih mudah untuk dianalisis dan diproses.

Cara Kerja PCA

1. Standarisasi Data
   Langkah pertama dalam PCA adalah menstandarisasi data. Hal ini penting karena PCA sangat sensitif terhadap skala variabel. Misalnya, jika satu fitur memiliki rentang nilai yang jauh lebih besar daripada fitur lain, maka fitur tersebut akan mendominasi hasil PCA. Untuk itu, kita harus menstandarisasi setiap fitur data sehingga memiliki rata-rata 0 dan deviasi standar 1.

2. Mencari Covariance Matrix
   Setelah data distandarisasi, langkah berikutnya adalah menghitung covariance matrix. Matriks ini menggambarkan seberapa besar hubungan antar fitur dalam data. Jika dua fitur memiliki nilai kovarians yang tinggi, artinya mereka memiliki hubungan yang kuat satu sama lain.

3. Menghitung Eigenvalues dan Eigenvectors
   Langkah selanjutnya adalah menghitung eigenvalues dan eigenvectors dari covariance matrix. Eigenvectors mewakili arah utama dari data, sementara eigenvalues menggambarkan seberapa besar variansi yang dapat dijelaskan oleh masing-masing eigenvector.

4. Memilih Komponen Utama
   Setelah memperoleh eigenvectors dan eigenvalues, kita akan memilih komponen utama berdasarkan eigenvalue terbesar. Komponen utama ini mewakili arah dengan variansi terbesar dalam data. Semakin besar eigenvalue, semakin penting komponen utama tersebut dalam menjelaskan variansi data.

5. Transformasi Data
   Langkah terakhir adalah memproyeksikan data ke dalam ruang baru berdasarkan komponen utama yang dipilih. Dengan demikian, data yang awalnya memiliki banyak dimensi dapat direduksi menjadi beberapa dimensi yang lebih sedikit namun tetap mengandung informasi yang penting.

Aplikasi PCA dalam Data Science

PCA memiliki berbagai aplikasi dalam data science dan machine learning, di antaranya:

1. Reduksi Dimensi
   PCA sering digunakan untuk mengurangi dimensi data sebelum diterapkan pada model machine learning. Pengurangan dimensi ini dapat membantu meningkatkan kinerja model dan mengurangi risiko overfitting.

2. Visualisasi Data
   Ketika kita bekerja dengan data yang memiliki banyak fitur, visualisasi menjadi sangat sulit. Dengan PCA, kita dapat mereduksi data menjadi 2 atau 3 dimensi, sehingga dapat divisualisasikan dalam bentuk grafik.

3. Penyaringan Fitur
   PCA dapat digunakan untuk memilih fitur-fitur yang paling penting dalam dataset, sehingga hanya fitur yang relevan yang digunakan untuk model analisis atau prediksi lebih lanjut.

4. Noise Reduction
   Dalam beberapa kasus, data dapat mengandung noise yang dapat mempengaruhi kinerja model. PCA dapat membantu mengurangi noise dengan fokus pada komponen utama yang memiliki variansi terbesar.

Kesimpulan

Principal Component Analysis (PCA) adalah teknik powerful dalam data science yang digunakan untuk mereduksi dimensi data dengan cara mengidentifikasi komponen utama yang menjelaskan variansi terbesar dalam data. Dengan memahami konsep dasar dan cara kerja PCA, kita dapat menggunakannya untuk meningkatkan kinerja analisis data dan model machine learning. Meskipun PCA bukan solusi yang cocok untuk semua jenis data, pemahaman yang baik tentang kapan dan bagaimana cara menggunakannya dapat sangat membantu dalam menyederhanakan masalah data yang kompleks.